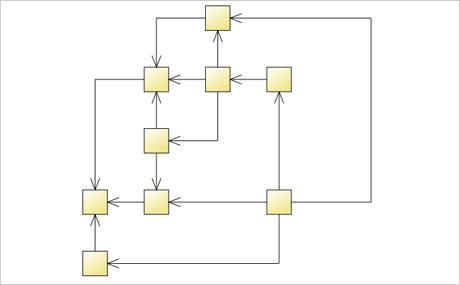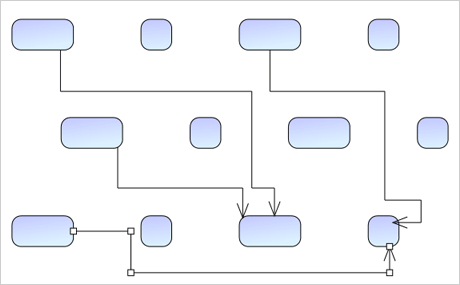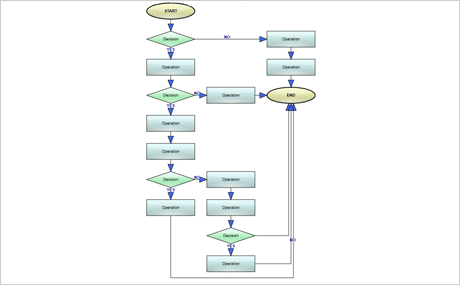
Download the sample for WPF in C#
Download the sample for WPF in VB.NET
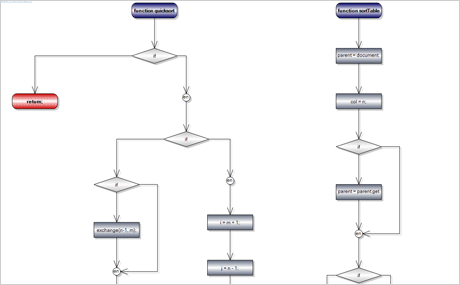
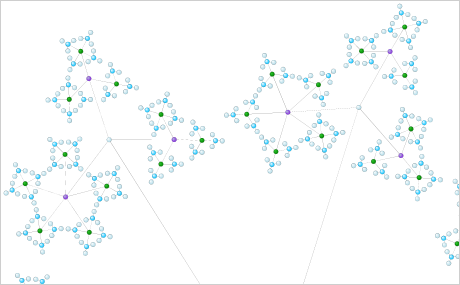
Download the sample for WPF in C#
Download the sample for WPF in VB.NET
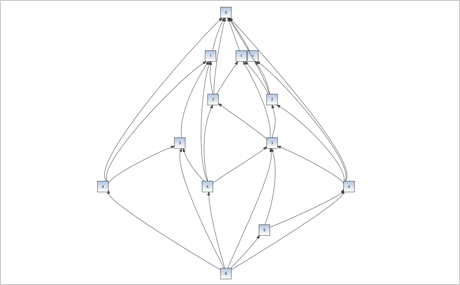

Download the sample for WPF in C#
Download the sample for WPF in VB.NET
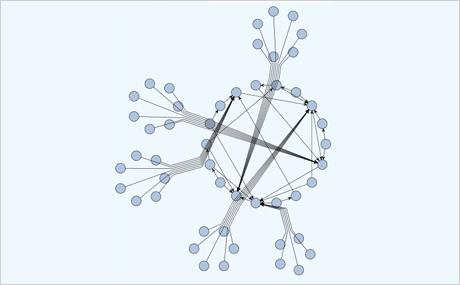
Download the sample for WPF in C#
Download the sample for WPF in VB.NET

Download the sample for WPF in C#
Download the sample for WPF in VB.NET
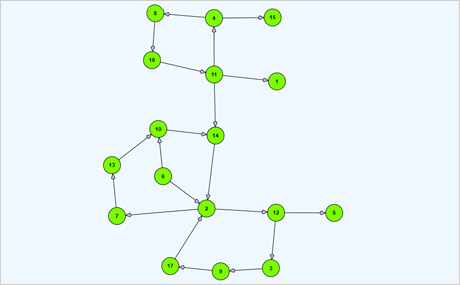
Download the sample for WPF in C#
Download the sample for WPF in VB.NET
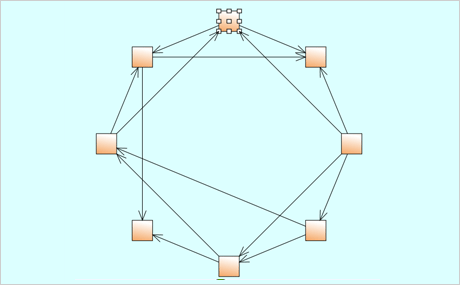
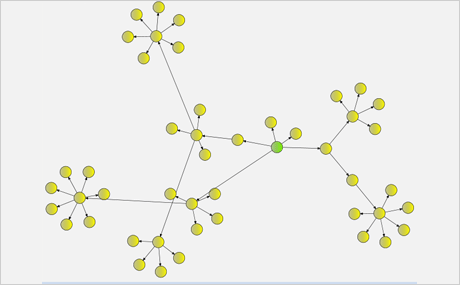
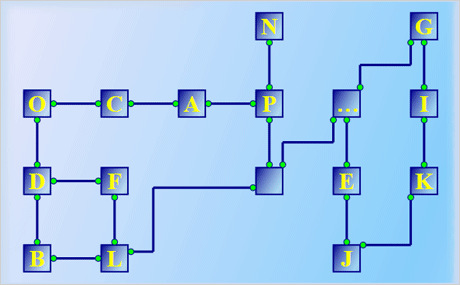
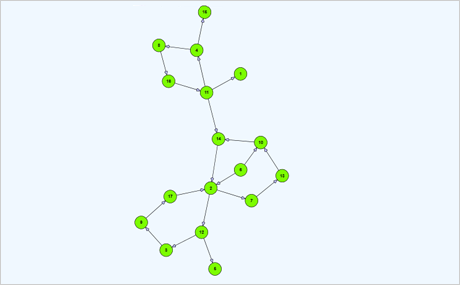
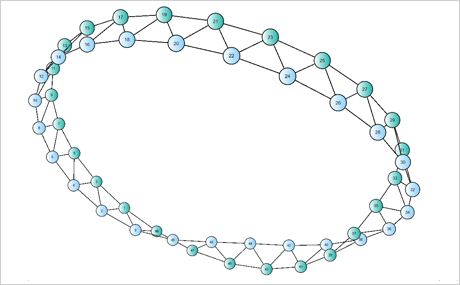
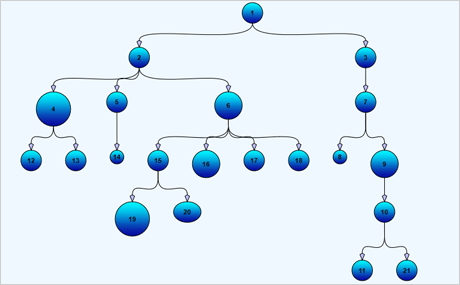
Download the sample for WPF in C#
Download the sample for WPF in VB.NET